

Réaction entre une solution d'acide fort et une solution de base forte
(Etude de la réaction entre une solution de chlorure d'hydrogène et une solution d'hydroxyde de sodium )
Départ
Addition progressive de soude
Réaction totale
Equivalence
Indicateurs colorés
Acide versé dans la base
Simulation
TP : Dosage de produits ménagers
![]()
On part d'une solution de HCl à Ca~0,1mol/L et on en prélève Va=10mL ; on ajoute ensuite de l'eau distillée pour obtenir environ 50mL, de façon à pouvoir tremper les électrodes.
La valeur théorique du pH de cette solution d'acide fort est : pH=-log C'a=-log 0,1/5~1,7
![]()
Addition progressive de soude :
En ajoutant progressivement de la soude ayant une
concentration Cb voisine de 0,1mol/L, on obtient la courbe suivante :
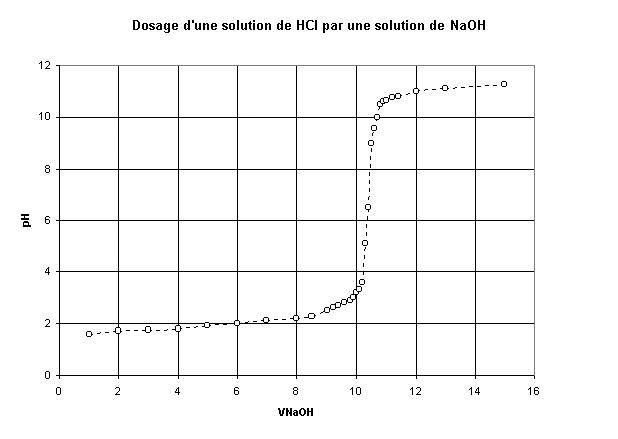
![]()
0<Vb<9mL : le pH obtenu montre qu'il se produit une réaction totale ; prenons, par exemple Vb=6mL :
| pH mesuré = 2,0 | |
| [H3O+]= 10-2 mol /L | |
| [OH-]= 10-14/10-2=10-12 mol/L | |
| nOH- présents dans le bécher = [OH-].Vt=10-12x(50+6)x10-3=5,6x10-14mol | |
| nOH- introduits = CbxVb=0,1x6x10-3mol |
Conclusion : les ions OH- introduits ont quasiment tous disparus
Il s'est produit une réaction totale :
Remarques :
| Cette réaction dégage 57,4 kJ/mol de OH- | |
| La réaction est en réalité réversible, mais très déplacée vers la gauche (la réaction inverse est l'autoprotolyse de l'eau) | |
| La réaction complète s'écrit : |
(H3O+ + Cl-) + (Na+ + OH-) --> 2H2O + (Na+ + Cl-) |
| Application : sachant que la réaction est totale, on peut calculer le pH pour un volume de soude versée ; par exemple, Vb=8mL |
| nH3O+initiaux = CaxVa = 0,1x10x10-3=10-3 mole | |
| nOH- introduits = CbxVb = 0,1x8x10-3 = 0,8x10-3 mole | |
| nOH-disparus = nOH- introduits = 0,8x10-3 mole | |
| nH3O+disparus = nOH-disparus = 0,8x10-3 mole | |
| nH3O+ restants = nH3O+initiaux - nH3O+disparus =10-3-0,8x10-3 = 0,2x10-3 | |
| [H3O+]= nH3O+ restants/Vt = 0,2x10-3/(50+8)x10-3 =3,4x10-3 mol/L | |
| pH= 2,5 |
![]()
| d'après l'équation bilan, à l'équivalence : |
|
| Le pH à l'équivalence, déterminé par la méthode des tangentes,
vaut 7 |
| En effet, à l'équivalence, nOH-versés = nH3O+initiaux
Or il disparait autant de H3O+ que de OH- , donc il reste dans la solution autant de l'un que de l'autre, d'où [H3O+] = [OH-] = 10-7mol/L |
| Cela explique l'utilisation d'indicateurs colorés pour déterminer le volume équivalent : |
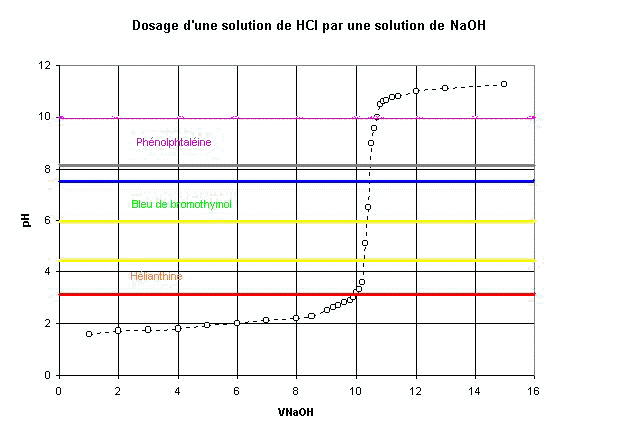
| Le meilleur indicateur coloré ici est le bleu de bromothymol, dont la zone de virage encadre le pH à l'équivalence, mais les deux autres indicateurs usuels donnent aussi un bon résultat ; | |
| ce n'est plus le cas si les solutions sont plus diluées. | |
| Retour au menu |
![]()
| Courbe de dosage d'une base forte par un acide fort : | |
| La courbe obtenue dans ce cas là est inversée par rapport à la précédente puisqu'on démarre en milieu basique ; à l'équivalence, le pH vaut 7, là aussi | |
| Retour au menu |
![]()