La chute du cycliste
Un cycliste se laisse aller dans une pente.
Problème ouvert.
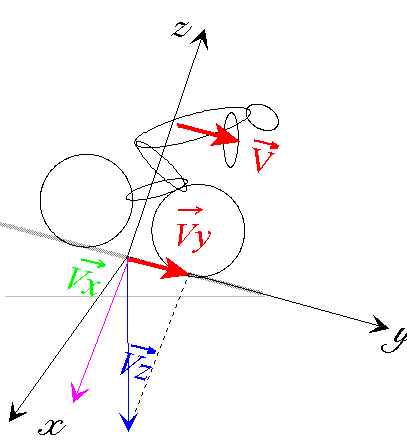
2 essais dans la même pente (Seine Port) (dénivelé : 30m sur 325m) puis un peu plus loin dans la pente de Sainte Assise (24m sur 325m).
Données dans le tableau :
'Données acquises par CAMPAGNE
données expérimentales :
constante expérimentale:
grandeurs calculées :
Données expérimentales
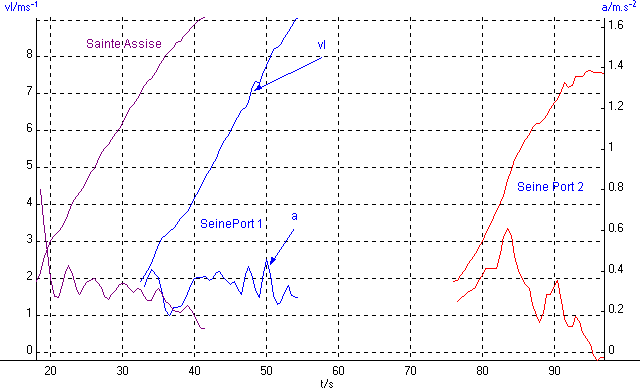
Le frottement paraît bien négligeable !
Modélisation de la vitesse :
Modèle sur vl=9.81*pente*ki*(t-t0) ( ki pour évaluer l'écart/pente théorique)
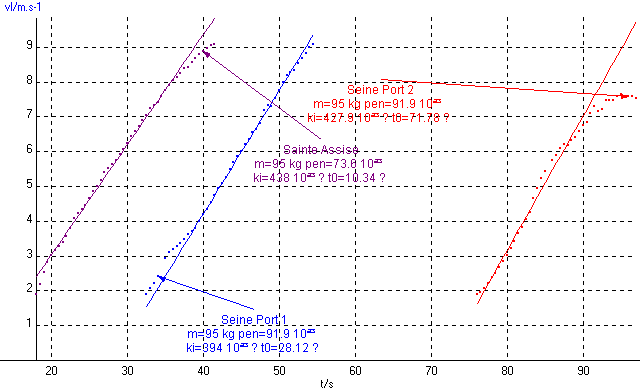
Est-ce que la pente de Seine Port est constante? Elle semble plus forte dans le bas (essai 2).
| page | m | pen | ki | t0 | |
| n° | kg | 10ª³ ? | s | ||
| 1 | 95 | 0.0919 | 0.394 | 2.812E4 | |
| 2 | 95 | 0.0919 | 0.4279 | 7.178E4 | |
| 3 | 95 | 0.0736 | 0.438 | 1.034E4 |
Dans ces circonstances, les valeurs approximatives de ki selon la carte d'état major seraient :
seine port : pen=sin(atan(30/325))=91,9.10-3
et sainte assise : pen=sin(atan(24/325))=73,6.10-3.
Le modèle linéaire fourni un rapport de ki fois plus faible : 0,394 0,428 et 0,438.
Le frottement serait-il fortement linéaire?
L'enregistrement est très sensible aux variations de pente.
Et ensuite :
Remonter à g, la pente ou déduire le frottement ?
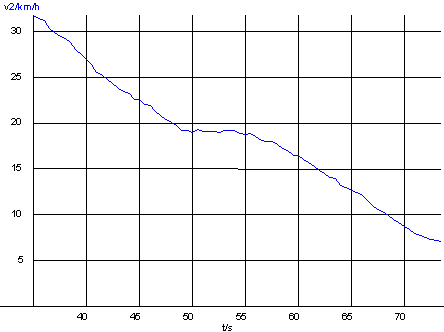
Recherche de g :
Si on modélise les forces de frottement, rien ne va plus! Trop d'imprécision dans les mesures ?
Pour les modéliser : faire un essai en décélération sur terrain plat.
(ci-contre un terrain pas assez plat...)
Expression des forces de frottement :
Si on suppose g connu et la pente parfaitement calibrée, c'est possible.
Une carte d'état major ou un géomètre seront nécessaires. Et la prise de mesure doit permettre l'identification exact des instants du passage dans la pente identifiée pour le bornage du modèle
L’apport du géomètre expert :
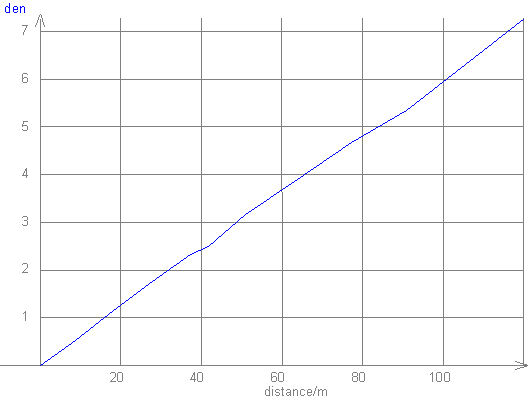
Un ami géomètre a réalisé pour nous le relevé du profil d’un pente située à
2,5 km du lycée (accessible à pied avec les élèves).
Nous obtenons un profil suivant :
den représente le dénivelé en m selon la distance de départ.
Le profil n’est pas parfaitement plan mais, grosso modo, on s ‘en accommodera !
La pente est de l’ordre de 6m pour 100m. (6%)
Il est alors possible d’évaluer les forces de frottement :
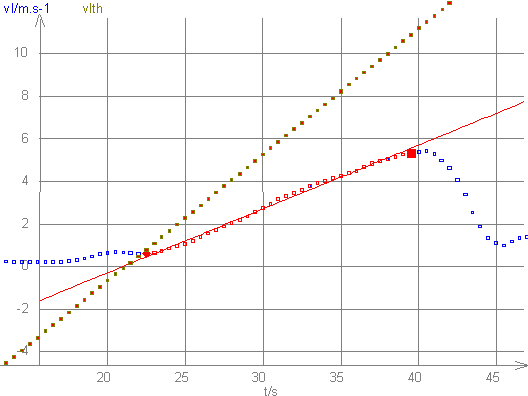Dans ce cas, la vitesse linéaire enregistrée (vl)
est 2 fois plus faible que la vitesse théorique (vlth) qu’on atteindrait sans
frottement (9.81*sin(alpha)*g) ; l’angle équivalent vaut :
arc sin-1=0.0305.
Les forces de frottement semblent très fortement constantes.
Pour un autre vélo , les mesures indiqueront un angle de 0.041 pour 0.0605.
La chaîne de mesure est analysée, nous sommes prêt à faire des mesures.