Le pendule est , en première approximation ,un
oscillateur harmonique.
Dans un repère galiléen un pendule simple est assimilable à un point matériel
soumis à une force de rappel proportionnelle à son élongation
Hypothèses :
Pour des raisons typographiques les vecteurs sont en caractères gras.
Le plan de figure est rapporté à un référentiel Galiléen
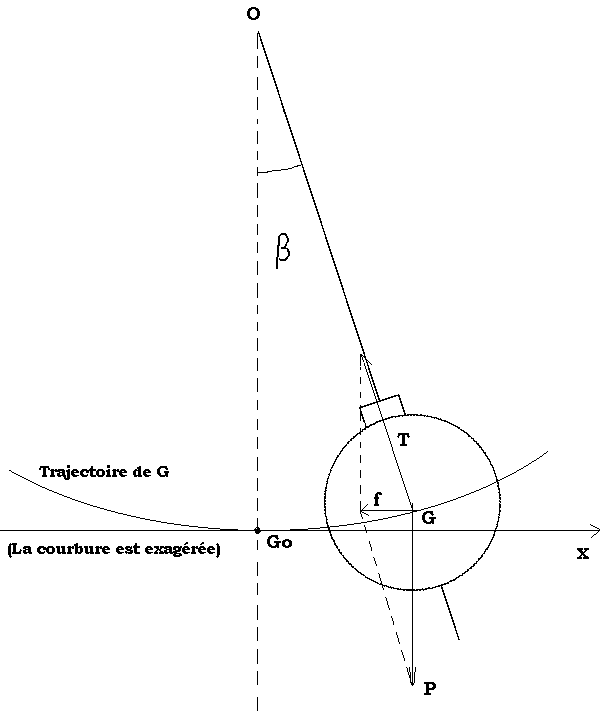
Analyse :
Pour le système « masse m » , dans le référentiel galiléen ci dessus , les forces
extérieures se réduisent à P = m.g , le poids ; et T la tension du
fil.
Le théorème du centre d’inertie : m.a = P + T
et P+ T = f , de norme f = m . g . tanß , soit f = m . g ß
Sur l’axe des x :
m . ax . i = - m . g .ß . i ( f est une force de rappel)
or ax = d²x / dt² et ß = x /L
en remplaçant d²x/dt² = - (g/L).x
ou d²x/dt² + (g/L) . x = 0
On reconnaît un oscillateur harmonique : d²x/dt² + wo².x =0
de pulsation : wo = sqrt( g / L) ( sqrt = racine carrée )
de période : To = 2.pi / wo T = 2.pi. sqrt( L / g)
Remarque : L’énergie potentielle du système doit se mettre comme pour
tout oscillateur harmonique sous la forme :
Ep = ½ . A . x² A étant une constante.
Ici Ep est l’énergie potentielle de pesanteur: Ep = m .g . h , en prenant
l’origine des altitudes h en Go .
Or h= m .g.L (1- cos ß) ; et ß est petit donc cos ß = 1-ß²/2 il vient :
Ep = ½ m . g .Lß²
et ß étant petit ß = x/L :
Ep = ½ m (g/L) . x²
ce qui est la forme cherchée. A= m. wo²