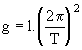Détermination de la densité du globe terrestre : (fin du 18e siècle)
Mesure de l'accélération de la pesanteur :
 |
Huygens (1629-1695) montre que, pour de faibles oscillations, la période d'un pendule simple ne dépend que de sa longueur et de l'accélération de la pesanteur (g) suivant la formule :
avec T : période d'oscillatios d'un pendule simple de longueur l. La mesure de la période permet de déterminer la valeur de g : g = 9,81 m.s-1. |
![[T=2*pi*sqrt(l/g)]](form1.gif)
d'où l'on tire 
Mesure de la constante universelle de la gravité :
 |
Newton (1642 -1727) a exprimé la loi d'attraction
gravitationnelle des masses :
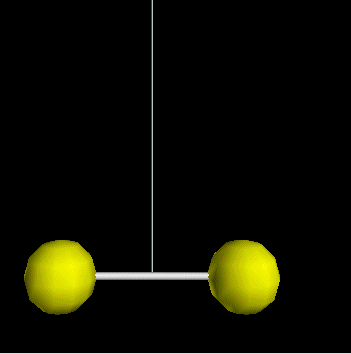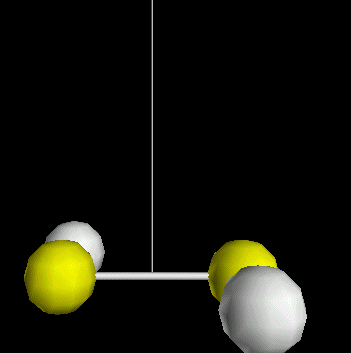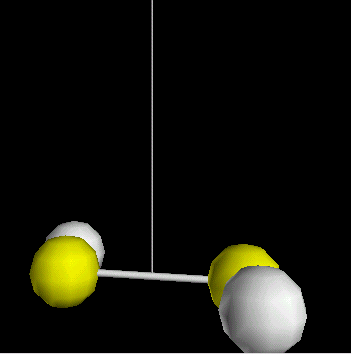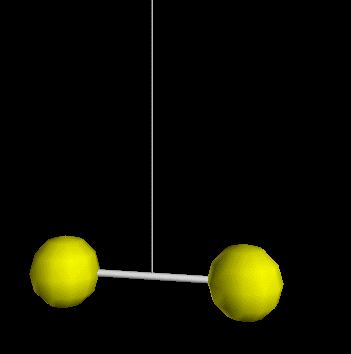
La mesure de la constante universelle de la gravité (G) a été réalisée avec un pendule de torsion : c'est l'expérience de Cavendish qui est schématisée sur la figure animée. Lorsque l'on approche les deux sphères représentées en gris, le pendule de torsion tourne d'un petit angle a, sous l'effet de l'attraction des masses. La mesure de cet angle a permet de calculer la force d'attraction F que l'on cherche à mesurer. La mesure de la force d'attraction entre les boules F a permis à Cavendish de déterminer la valeur de G. G = 6,67.10-11 N.m-2.kg-2 |
avec m et m' : masses des objets séparés par la distance d et s'attirant par
la force F. G est la constante universelle de la gravitation.Calcul de la masse du globe terrestre
En utilisant la formule de la loi de Newton appliquée à un objet de masse m se trouvant à la surface du globe terrestre de rayon Rt et de masse Mt, Cavendish a pu déterminer la masse du globe terrestre :
![[F=mg=G*m*Mt/Rt^2 et donc g=G*Mt/Rt^2]](form2.gif){kind=small}
. (1)
Le rayon du globe terrestre est d'environ 6370 km soit 6,37.106 m.
de (1), on tire ![[Mt=g*Rt^2/G=5,97E24 kg]](form3.gif){kind=small}
Détermination de la densité du globe terrestre : (Cavendish - 1798)
Le volume terrestre est : ![[Vt=4/3 *pi*Rt^3 = 1,083E21 m3]](form4.gif){kind=small}
Sa masse volumique moyenne est donc de ![[Mt/Vt=5500 kg.m-3]](form5.gif){kind=small}
(5,5 g.cm-3)
La masse volumique des roches de la surface du globe est comprise entre 2 et 3 (2,5 à 2,7 dans la plupart des cas). On est loin de la densité moyenne déterminée par Cavendish. Il faut donc faire l'hypothèse d'une couche profonde beaucoup plus dense (on parle parfois au 19e siècle de plomb ou même d'or).
La mesure de Cavendish est le premier résultat scientifique montrant que la structure interne du globe n'est pas homogène.
Rédigé par : Jean-François Madre (e-mail : jean-francois.madre@wanadoo.fr)